Introduction

Dining Philosophers is a classic problem that was first introduced by famous computer scientist Edsger Dijkstra for an exam exercise, built around the concept of multiple computers competing for access to peripherals [1]. However it was only formalised with the philosophers much later by Sir Tony Hoare, most famous for his invention of the quick sort algorithm [2].

The problem, especially considering Dijkstra’s original exam question, is designed to depict synchronisation issues in concurrent systems and how deadlocks can occur, demonstrating mechanisms for avoiding them.

The Problem

The problem revolves around five philosophers sitting at a round table. Separating each philosopher on either side is a fork. To avoid starvation, the philosophers must eat, and whilst not, they must think. To eat, a philosopher must have both his left and right fork in either hand.

[3] Dining Philosophers

However, this is where the problem occurs. Say each philosopher has picked up their left fork. This is where a deadlock has transpired. None of the philosophers can eat, as their right fork has been picked up by the philosopher to their right, and they are all stuck in a state of limbo waiting for their right fork, and hence, they starve to death.

When originally conceived in 1965, the difficulties were often related to access to external peripherals such as tape drives, however these hazards of deadlocks and synchronisation are amplified in many more complex scenarios such as database access and lower level kernel operations.

Solution

What happens if we take one philosopher out of the picture, yet leave the same number of forks? At least one philosopher will be able to eat, and when finished, the next one and so forth that is waiting to acquire one of the forks that the first philosopher had been using an so forth. However, this would be unfair to the philosopher removed from the picture, and they would eventually starve.

To counter this, we introduce mediator, a waiter so to speak. If the waiter only allows up to four of the five philosophers the option to pick up the fork, then we have solved the first part of the problem. Once the first philosopher has finished eating and has returned to think signalling the waiter that he has finished, then the unlucky philosopher that was not allowed to reach for his forks can begin, and the first one will have to wait.

Solution Design

A solution using the aformentioned approach involving a mediator was developed using C#.

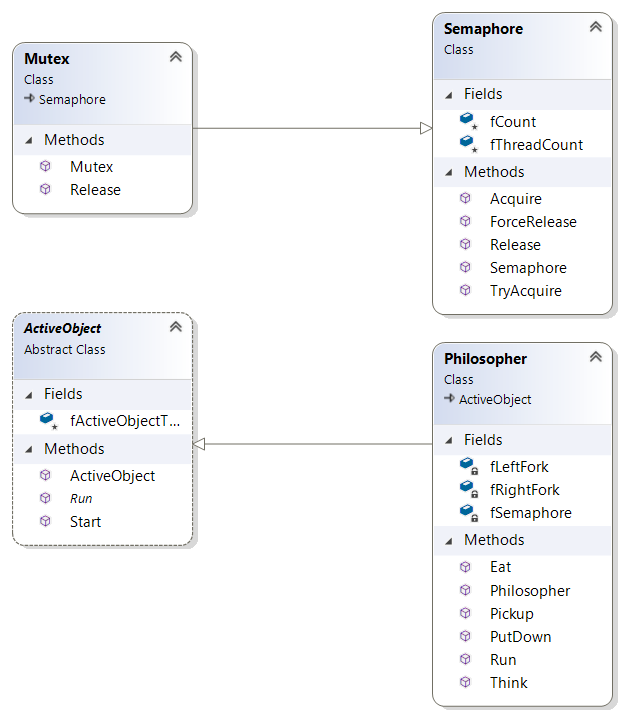
Active Object

An abstract class designed to conceal the thread that it’s built upon for the classes that implements it. Has the option to be started when instantiated. The thread allows the objects to run concurrently with others. It also receives a name.

Semaphore

A semaphore is a a synchronization object used to control permissions via a number of tokens specified upon instantiation. Objects can acquire the semaphore, but when it has run out of tokens, they must wait for another object to release the semaphore, making another token available for use. Both the release and acquire methods are locked to avoid synchronisation issues. The concept was first introduced in the early 1960s by Edsger Dijkstra [4].

In this scenario, the waiter is a semaphore with four tokens. Each philosopher must acquire the waiter, before proceeding to pick up the fork.

Mutex

A mutex is an implementation of the semaphore with only a single token, thus creating a binary semaphore. Each fork is a semaphore, as only one philosopher can acquire it at a time.

Philosopher

The philosopher is an object that takes three references. Two mutex’s signalling the left and right fork, and a semaphore, for the waiter. It begins by thinking, then will attempt to pickup the forks, by first acquiring the waiter, and then each fork. Once it has acquired the semaphore and then the two mutexs, it will eat, and then release them. This cycle will run indefinitely.

Conclusion

The Dining Philosopher problem is a classic example detailing on a high level how concurrency issues can be very problematic in computing, with the mediator demonstrating one simple way that it can be overcome. However, this is not the most efficient method, and work could be done to improve the solution so that the optimal number of forks are in use at any given time.

References

• [1] E. Dijkstra, “EWD1000”, Austin, 1987.
• [2] C. Hoare, Communicating Sequential Processes. Englewood Cliffs (New Jersey): Prentice-Hall, 1985.
• [3] B. Esham, An illustration of the dining philosophers problem. 2005.
• [4] E. Dijkstra, “EWD35”, Austin.
  
  The source code can be found here.